Les gosses le savent : nos explications sont décevantes, toujours.

• Pourquoi papy a eu un accident ? me demande Jonas.
• Parce qu’il roulait trop vite.

Mais cette réponse n’est vraiment éclairante que s’il sait pourquoi papy allait trop vite.

• Pourquoi papy allait trop vite ?

J’évoque le fait qu’il boit un peu trop, et méprise les limitations de vitesse, mais cela continue.

• Pourquoi ?
• Pourquoi ?
• …

En général, je me lasse avant lui et renonce à expliquer l’existence des premiers hominidés ou la sortie des poissons de l’océan. D’autres parents, peut-être moins naturalistes que moi, finissent par invoquer la volonté de Dieu. Ils récoltent invariablement un,

• Qui a créé Dieu ?

Quand ils commencent à se douter que leur vie n’est pas infinie et qu’ils n’arriveront jamais à la fin de leurs questions, cependant, les enfants se lassent aussi. Ils deviennent grands. Ils se font une raison. On doit toujours s’arrêter sur un :

• Parce que c’est comme ça un point c’est tout.

Nos explications sont décevantes et on ne peut rien y faire, point. Les enfants le savent bien.

La quête d’une explication complète et le trilemme des métaphysiciens

Il existe cependant une poignée d’êtres à part qui grandissent à peu près normalement, mais ne renoncent pas à leurs ambitions enfantines. Les cosmologistes, quelques chercheurs en physique théorique, les métaphysiciens. Ces derniers ont d’ailleurs produit un argument fascinant qui repose sur le principe (appelé depuis Leibniz « principe de raison suffisante ») que chaque chose doit avoir une explication, et qu’il doit donc exister des explications satisfaisantes: des “explications complètes” (c’est le terme qu’ils utilisent), qui ne s’arrêtent pas sur un “parce que c’est comme ça un point c’est tout” et éliminent complètement l’arbitraire.

Mais raisonnent-ils, si l’on part d’un événement E₁, disons l’accident de papy, et qu’on en trouve une explication E₂, et si on trouve une explication E3 de E2, etc., et si on suppose que tout a bien une explication, seules trois possibilités s’offrent à nous:

• Soit on continue ainsi jusqu’à l’infini : E₁ est expliqué par E₂ qui est expliqué par … qui est expliqué par E_n, qui est expliqué par E_n+1, qui est expliqué par …
• Soit notre explication se mord la queue, par exemple E₁ est expliqué par E₂ qui est expliqué par E₃ qui est lui-même expliqué par E₁ !
• Soit notre explication s’arrête sur quelque chose qui s’auto-explique : par exemple E₁ est expliqué par E₂ qui est expliqué par E₃ qui est expliqué par E₃ lui-même !

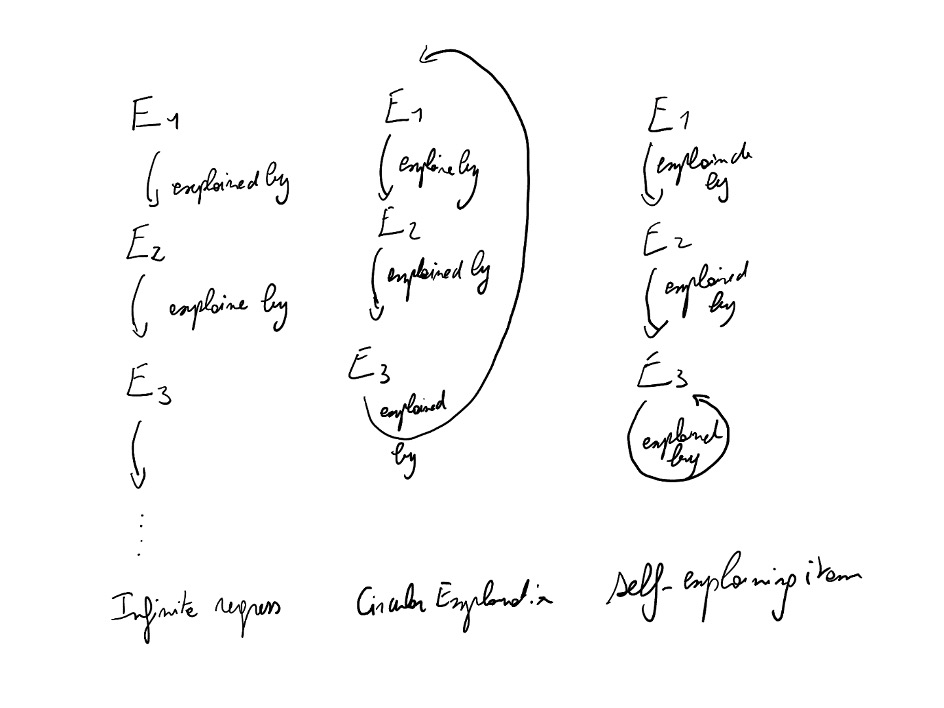
L’argument cosmologique pour l’existence de Dieu

Les deux premières options ont presque toujours été rejetées. De nombreux philosophes nient que les explications circulaires ou infinies puissent être de vraies explications. Les autres, plus prudemment, admettent que ce sont des explications acceptables, mais ils nient qu’elles puissent fournir des explications complètes, entièrement satisfaisantes. Si, pour prendre le cas des séries explicatives infinies sur lequel je vais me concentrer ici, E₁ est expliqué par E₂ qui est expliqué par… qui est expliqué par E_n, etc. Chaque événement E_i est bien expliqué par le suivant, mais la série infinie elle-même n’est pas expliquée. C’est le sens d’un argument célèbre de Leibniz, qui imagine une série infinie de scribes recopiant chacun le livre du suivant. Supposons que le premier scribe ait copié la Bible parce que le second avait aussi recopié la Bible, parce que, etc. Dans cette série infinie, le fait que n’importe quel scribe ait recopié la bible s’explique par le fait qu’il recopiait le livre du scribe suivant qui avait lui-même recopié la Bible… Mais cette série d’explications laisse quelque-chose d’arbitraire. Elle n’explique pas, en effet, pourquoi ils ont tous recopié la Bible plutôt que les Éléments de Géométrie. Une autre manière de le dire est que chaque événement est bien expliqué par le suivant, mais l’ensemble des événements (ils ont tous recopié la Bible) ne l’est pas et notre explication n’est pas complète. Le problème vient, semble-t-il, du fait que la série d’explications laisse le contenu du livre recopié complètement indéterminé et n’élimine donc pas complètement l’arbitraire. 

Du caractère incomplet des explications infinies (ou circulaires), bien des philosophes ont conclu qu’il devait exister quelque chose d’absolument fondamental qui s’explique soi-même. Ne voyant rien d’autre que Dieu pour s’expliquer soi-même et expliquer tout le reste, beaucoup en ont conclu que Dieu devait exister pour qu’on ait des explications satisfaisantes. On parle de l’argument cosmologique pour l’existence de Dieu. On trouve des variantes de cet argument dès les premiers métaphysiciens.

Les philosophes plus naturalistes, qui considèrent l’existence de Dieu ou même d’une chose qui s’auto-explique avec suspicion, ont eu tendance à renoncer aux ambitions métaphysiques enfantines d’une explication pleinement satisfaisante. Les explications buteront toujours sur de l’inexpliqué, et le mieux que l’on puisse faire est de faire en sorte que cet inexpliqué ne soit pas trop étrange, et ne réclame pas avec trop d’insistance une explication qu’on ne sera pas en mesure de lui trouver.

Des explications complètes sans Dieu ni entité auto-explicative

Dans l’article Are infinite explanations self-explanatry? qui vient de paraître dans la revue Erkentnis, je tente de venger les philosophes naturalistes qui n’auraient pas renoncé aux espoirs enfantins d’une explication complète. Plus précisément, je montre, contre Leibniz, que les explications infinies ou circulaires peuvent être complètes, et faire mieux que les explications théistes.

Mon argument repose sur un certain nombre d’exemples d’explications infinies et complètes – je vais présenter l’un d’eux ci-dessous – mais je ne suis pas arrivé à ces contre-exemples par hasard et je peux dire ici quelque chose sur la manière dont je les ai trouvés. J’ai reçu une formation d’ingénieur avant de devenir philosophe, et dans les sciences fondamentales, on n’utilise presque jamais les notions d’explications ou de causes. On y substitue plutôt une notion qui précise grandement celles-ci, celle de dépendance fonctionnelle. En substituant cette notion de dépendance fonctionnelle à celle d’explication, on peut aisément réaliser ce qui ne va pas dans l’argument de Leibniz, et comprendre que les explications infinies ou circulaires peuvent, dans certains cas, être complètes. Ci-dessous, j’explique cette idée de dépendance fonctionnelle puis j’expose l’exemple clef de l’article.

Dépendance fonctionnelle

En science fondamentale, lorsqu’un événement E₂ explique un autre E₁, les paramètres qui spécifient ces deux événements sont liés par des équations mathématiques qui permettent de déduire à partir d’. Mieux que cela, les paramètres spécifiant dépendent fonctionnellement des paramètres spécifiant : il y a une fonction mathématique telle que . 

Prenons un exemple simple. L’événement “cette balle est lâchée à h mètres du sol” explique l’événement “lorsqu’elle heurte le sol, elle a la vitesse v”. La vitesse de chute (qui spécifie l’événement ) est reliée à la hauteur du lâcher de la balle (qui spécifie l’événement ) par l’équation suivante, dérivée des lois de Newton (je l’écris en langage naturel):

• la vitesse au carré est égale à 2 fois la hauteur multipliée par g

(où est une constante environ égale à 9,81) 

Et les paramètres du premier événement (E₁) dépendent fonctionnellement de ceux (h) du second (E₂) :

• la vitesse est égale à la racine carrée de 2 fois la hauteur multipliée par g

En remplaçant la notion vague d’explication par cette notion bien plus précise de dépendance fonctionnelle, j’ai trouvé des conditions générales sur le type de dépendance fonctionnelle entre les événements E₁, E₂, …, E_n, … pour qu’on ait une série explicative infinie ou circulaire, mais complète. Dans cet article, j’ai cependant passé ces conditions générales sous silence, car je n’étais pas parvenu à leur trouver une formulation mathématiquement élégante, et je n’avais ni la place ni les ressources pour relier cette notion de dépendance fonctionnelle aux théories philosophiques classiques des explications. J’ignorais en, particulier, qu’il existe une théorie des explications très féconde et peut-être bien aujourd’hui dominante qui repose sur une idée très proche de celle de dépendance fonctionnelle, le “structural equations account” (cf. e.g. Schaffer 2015). J’ai réparé ces deux lacunes dans un article soumis récemment à une autre revue et actuellement en révision.

Un contre-exemple à l’idée que les explications infinies sont toujours incomplètes

Je peux maintenant présenter le plus simple de mes contre-exemples à l’idée que les explications infinies sont toujours incomplètes, sinon carrément vicieuses (je vais ignorer le cas des explications circulaires jusqu’à la fin de ce post). Ce contre-exemple s’inspire de la série de scribes de Leibniz. Nous l’avons vu, si l’on considère que la série entière n’est pas expliquée, dans ce cas, et que l’explication est in fine incomplète, c’est que celle-ci laisse le contenu des livres indéterminés. Le fait que chaque scribe copie le livre du suivant laisse en effet entièrement ouvert le contenu du livre qu’ils copient. Si on trouvait un exemple où au contraire, le fait que chaque E_i s’explique par le suivant détermine entièrement tous les paramètres de la série des (E_i), alors on aurait vraisemblablement une explication complète.

Considérez, au lieu d’une infinité de scribes, une infinité d’ajusteurs et un bâton ou “stick” en plastique mou de taille finie. Comme les scribes de Leibniz les ajusteurs se comportent tous, toujours, de la même manière. Quand on leur passe un stick, ils l’ajustent pour que sa taille se rapproche de 1. Plus précisément, si le stick qu’on leur passe à une longueur  l , ils l’étirent ou il le compriment de manière à produire (et à passer à l’ajusteur suivant) un stick de longueur l+\frac{1-l}{2} . La taille l_1du stick  que le premier ajusteur reçoit du deuxième s’explique par celle, l_2, du stick que le deuxième ajusteur a reçu du troisième, et on a l_1=l_2+\frac{1-l_2}{2}. De la même manière la taille du stick que le deuxième ajusteur a reçu s’explique par celle du stick reçu par le troisième ajusteur a reçu : l_2=l_3+\frac{1-l_3}{2}, etc. On peut montrer que l_1=l_i+\frac{1-l_i}{2^i}. Intuitivement, à chaque passage par un ajusteur de stick la taille du stick se rapproche de plus en plus de 1. On peut aussi montrer  que si la série est infinie, alors nécessairement tous les sticks sont de longueur 1 :  l_1=l_2=…=l_i=…=1. À la différence du cas des scribes de Leibniz, où chaque terme de la série est expliqué par le suivant, mais où la série dans son entier reste indéterminée (il pourrait s’agir d’une série de copies de a Bible ou des Eléments de Géométrie) et, semble-t-il, inexpliquée, on a ici un cas où les explications de chaque terme par le suivant déterminent la série dans son entier. Le fait que chaque terme explique le suivant rend nécessaire que tous les termes soient des sticks de longueur 1. Je montre plus rigoureusement dans l’article que cela justifie l’idée que la série dans son entier est bien expliquée et qu’on a une explication complète. Un autre point à noter est que si la série ne descendait pas jusqu’à l’infini mais s’arrêtait, disons, au 456^ème ajuster de stick, alors la taille des sticks resterait indéterminée. Le dernier stick pourrait en effet avoir n’importe quelle taille. L’infini est ici essentiel à l’obtention d’une explication complète.   

Bien sûr, cet exemple est trivial. Les ajusteurs de sticks n’existent pas et s’ils existaient, ils constitueraient tout au plus une curiosité. Il n’en reste pas moins que cet exemple montre que les explications qui vont à l’infini (les philosophes parlent de régression à l’infini) ne sont pas toujours un problème. Mieux, il montre que la descente à l’infini peut constituer un véritable atout, puisqu’elle permet d’obtenir une explication complète que l’on n’obtiendrait pas avec une série finie.

Je montre par ailleurs dans l’article que les explications infinies ne peuvent pas être exclues au nom de la physique moderne et qu’elles sont plus communes qu’on ne le croit en science. Elles fournissent ainsi de sérieux concurrents aux explications théistes du monde.

Enfin, les explications infinies et complètes peuvent être très simples et très élégantes, et satisfaire ainsi la curiosité des enfants qui ne croient pas en Dieu – mais qui ont étudié un peu les mathématiques. 

Cela m’amène à une question importante que je n’aborde pas dans l’article : pourquoi les philosophes n’ont-ils pas vu qu’il pouvait y avoir des explications complètes infinies ? C’est, malheureusement, il me semble, parce qu’il faut un peu de rigueur et de mathématiques pour préciser la notion vague d’explication en termes de détermination fonctionnelle et arriver à réaliser cela. Or, depuis près d’un siècle, les philosophes qui visent la rigueur s’inspirent bien plus de la logique que des mathématiques. 

Références 

Billon, Alexandre (2021). Are infinite explanations self-explanatory? Erkenntnis 88 (5):1935-1954.

Schaffer, J. (2016) Grounding in the image of causation. Philos Stud 173, 49–100. https://doi.org/10.1007/s11098-014-0438-1